bayesml.contexttree package

bayesml.contexttree package#

Module contents#

The stochastic data generative model is as follows:

\(\mathcal{X}=\{1,2,\ldots,K\}\) : a space of a source symbol
\(x^n = x_1 x_2 \cdots x_n \in \mathcal{X}^n~(n\in\mathbb{N})\) : an source sequence
\(D_\mathrm{max} \in \mathbb{N}\) : the maximum depth of context tree models
\(T\) : a context tree model, \(K\)-ary regular tree whose depth is smaller than or equal to \(D_\mathrm{max}\), where “regular” means that all inner nodes have \(K\) child nodes
\(\mathcal{T}\) : a set of \(T\)
\(s\) : a node of a context tree model
\(\mathcal{I}(T)\) : a set of inner nodes of \(T\)
\(\mathcal{L}(T)\) : a set of leaf nodes of \(T\)
\(\mathcal{S}(T)\) : a set of all nodes of \(T\), i.e., \(\mathcal{S}(T) = \mathcal{I}(T) \cup \mathcal{L}(T)\)
\(s_T(x^{n-1}) \in \mathcal{L}(T)\) : a leaf node of \(T\) corresponding to \(x^{n-1} = x_1 x_2\cdots x_{n-1}\)
\(\boldsymbol{\theta}_s = (\theta_{1|s}, \theta_{2|s}, \ldots, \theta_{K|s})\) : a parameter on a leaf node, where \(\theta_{k|s}\) denotes the occurrence probability of \(k\in\mathcal{X}\)

\[p(x_n | x^{n-1}, \boldsymbol{\theta}_T, T)=\theta_{x_n|s_T(x^{n-1})}.\]

The prior distribution is as follows:

\(g_{0,s} \in [0,1]\) : a hyperparameter assigned to \(s \in \mathcal{S}(T)\)
\(\beta_0(k|s) \in\mathbb{R}_{>0}\) : a hyperparameter of the Dirichlet distribution
\(\boldsymbol{\beta}_0(s) = (\beta_0(1|s), \beta_0(2|s), \ldots, \beta_0(K|s)) \in\mathbb{R}^{K}_{>0}\)
\(C(\boldsymbol{\beta}_0(s)) = \frac{\Gamma\left(\sum_{k=1}^{K} \beta_0(k|s)\right)}{\prod_{k=1}^{K} \Gamma\left(\beta_0(k|s)\right)}\)

For \(\boldsymbol{\theta}_s\) on \(s\in\mathcal{L}(T)\), the Dirichlet distribution is assumed as the prior distribution as follows:

\[p(\boldsymbol{\theta}_s|T) = \mathrm{Dir}(\boldsymbol{\theta}_s|\,\boldsymbol{\beta}_0(s)) = C(\boldsymbol{\beta}_0(s)) \prod_{k=1}^{K} \theta_{k|s}^{\beta_0(k|s)-1}.\]

For \(T \in \mathcal{T}\),

\[p(T)=\prod_{s \in \mathcal{I}(T)} g_{0,s} \prod_{s' \in \mathcal{L}(T)} (1-g_{0,s'}),\]

where \(g_{0,s}=0\) if the depth of \(s\) is \(D_\mathrm{max}\).

The posterior distribution is as follows:

\(g_{n,s} \in [0,1]\) : the updated hyperparameter
\(T_\mathrm{max}\) : a superposed context tree, \(K\)-ary perfect tree whose depth is \(D_\mathrm{max}\)
\(s_\lambda\) : the root node
\(\beta_n(k|s) \in\mathbb{R}_{>0}\) : a hyperparameter of the posterior Dirichlet distribution
\(\boldsymbol{\beta}_n(s) = (\beta_n(1|s), \beta_n(2|s), \ldots, \beta_n(K|s)) \in\mathbb{R}^{K}_{>0}\)
\(I \{ \cdot \}\): the indicator function

For \(\boldsymbol{\theta}_s \in\mathcal{L}(T_\mathrm{max})\),

\[p(\boldsymbol{\theta}_s|x^n) = \mathrm{Dir}(\boldsymbol{\theta}_s|\,\boldsymbol{\beta}_n(s)) = C(\boldsymbol{\beta}_n(s)) \prod_{k=1}^{K} \theta_{k|s}^{\beta_n(k|s)-1},\]

where the updating rule of the hyperparameter is as follows:

\[\beta_n(k|s) = \beta_0(k|s) + \sum_{i=1}^n I \left\{ s \ \mathrm{is \ the \ ancestor \ of} \ s_{T_\mathrm{max}}(x^{i-1}) \ \mathrm{and} \ x_i=k \right\}.\]

For \(T \in \mathcal{T}\),

\[p(T|x^{n-1})=\prod_{s \in \mathcal{I}(T)} g_{n,s} \prod_{s' \in \mathcal{L}(T)} (1-g_{n,s'}),\]

where the updating rules of the hyperparameter are as follows:

\[\begin{split}g_{n,s} = \begin{cases} g_{0,s}, & n=0, \\ \frac{ g_{n-1,s} \tilde{q}_{s_{\mathrm{child}}} (x_n|x^{n-1}) } { \tilde{q}_s(x_n|x^{n-1}) } & \mathrm{otherwise}, \end{cases}\end{split}\]

where \(s_{\mathrm{child}}\) is the child node of \(s\) on the path from \(s_\lambda\) to \(s_{T_\mathrm{max}}(x^n)\) and

\[\begin{split}\tilde{q}_s(x_n|x^{n-1}) = \begin{cases} q_s(x_n|x^{n-1}) & s\in\mathcal{L}(T_\mathrm{max}), \\ (1-g_{n-1,s}) q_s(x_n|x^{n-1}) + g_{n-1,s} \tilde{q}_{s_{\mathrm{child}}}(x_n|x^{n-1}) & \mathrm{otherwise}. \end{cases}\end{split}\]

Here,

\[q_s(x_n|x^{n-1}) = \frac{ \beta_{n-1}(x_n|s) } {\sum_{k'=1}^{K} \beta_{n-1}(k'|s)}.\]

The predictive distribution is as follows:

\(\boldsymbol{\theta}_\mathrm{p} = (\theta_{\mathrm{p},1}, \theta_{\mathrm{p},2}, \ldots, \theta_{\mathrm{p},K})\) : a parameter of the predictive distribution, where \(\theta_{\mathrm{p},k}\) denotes the occurrence probability of \(k\in\mathcal{X}\).

\[p(x_n|x^{n-1}) = \theta_{\mathrm{p},x_n},\]

where the updating rule of the parameters of the pridictive distribution is as follows.

\[\theta_{\mathrm{p}, k} = \tilde{q}_{s_\lambda}(k|x^{n-1})\]

References

Matsushima, T.; and Hirasawa, S. Reducing the space complexity of a Bayes coding algorithm using an expanded context tree, 2009 IEEE International Symposium on Information Theory, 2009, pp. 719-723, https://doi.org/10.1109/ISIT.2009.5205677
Nakahara, Y.; Saito, S.; Kamatsuka, A.; Matsushima, T. Probability Distribution on Full Rooted Trees. Entropy 2022, 24, 328. https://doi.org/10.3390/e24030328

class bayesml.contexttree.GenModel(c_k, c_d_max=2, root=None, h_g=0.5, h_beta_vec=None, h_root=None, seed=None)#

Bases: Generative

The stochastice data generative model and the prior distribution

Parameters:

c_kint: A positive integer
c_d_maxint, optional: A positive integer, by default 10
rootcontexttree._Node, optional: A root node of a context tree, by default a tree consists of only one node.
h_gfloat, optional: A real number in \([0, 1]\), by default 0.5
h_beta_vecnumpy.ndarray, optional: A vector of positive real numbers, by default [1/2, 1/2, … , 1/2]. If a single real number is input, it will be broadcasted.
h_rootcontexttree._Node, optional: A root node of a superposed tree for hyperparameters by default None
seed{None, int}, optional: A seed to initialize numpy.random.default_rng(), by default None

Methods

`gen_params`([tree_fix])	Generate the parameter from the prior distribution.
`gen_sample`(sample_length[, initial_values])	Generate a sample from the stochastic data generative model.
`get_constants`()	Get constants of GenModel.
`get_h_params`()	Get the hyperparameters of the prior distribution.
`get_params`()	Get the parameter of the sthocastic data generative model.
`load_h_params`(filename)	Load the hyperparameters to h_params.
`load_params`(filename)	Load the parameters saved by `save_params`.
`save_h_params`(filename)	Save the hyperparameters using python `pickle` module.
`save_params`(filename)	Save the parameters using python `pickle` module.
`save_sample`(filename, sample_length[, ...])	Save the generated sample as NumPy `.npz` format.
`set_h_params`([h_g, h_beta_vec, h_root])	Set the hyperparameters of the prior distribution.
`set_params`([root])	Set the parameter of the sthocastic data generative model.
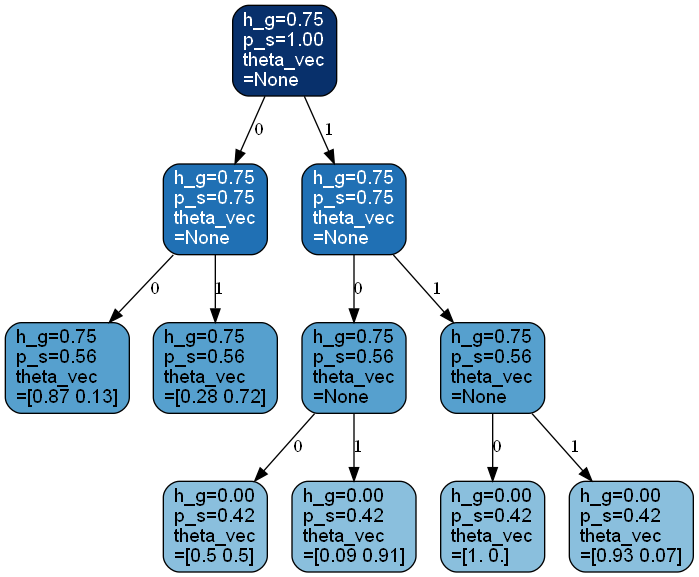
`visualize_model`([filename, format, ...])	Visualize the stochastic data generative model and generated samples.

get_constants()#

Get constants of GenModel.

Returns:

constantsdict of {str: int, numpy.ndarray}

"c_k" : the value of self.c_k
"c_d_max" : the value of self.c_d_max

set_h_params(h_g=None, h_beta_vec=None, h_root=None)#

Set the hyperparameters of the prior distribution.

Parameters:

h_gfloat, optional: A real number in \([0, 1]\), by default None
h_beta_vecnumpy.ndarray, optional: A vector of positive real numbers, by default None
h_rootcontexttree._Node, optional: A root node of a superposed tree for hyperparameters by default None

get_h_params()#

Get the hyperparameters of the prior distribution.

Returns:

h_paramsdict of {str: float, numpy.ndarray, contexttree._Node}

"h_g" : the value of self.h_g
"h_beta_vec" : the value of self.h_beta_vec
"h_root" : the value of self.h_root

gen_params(tree_fix=False)#

Generate the parameter from the prior distribution.

The generated vaule is set at self.root.

Parameters:

tree_fixbool: If True, tree shape will be fixed, by default False.

set_params(root=None)#

Set the parameter of the sthocastic data generative model.

Parameters:

rootcontexttree._Node, optional: A root node of a contexttree, by default None.

get_params()#

Get the parameter of the sthocastic data generative model.

Returns:

paramsdict of {str:float}

"root" : The value of self.root.

gen_sample(sample_length, initial_values=None)#

Generate a sample from the stochastic data generative model.

Parameters:

sample_lengthint: A positive integer
initial_valulesnumpy ndarray, optional: 1 dimensional int array whose size coincide with self.c_d_max, by default None. Its elements must be in [0,c_k-1]

Returns:

xnumpy ndarray: 1 dimensional int array whose size is sammple_length.

save_sample(filename, sample_length, initial_values=None)#

Save the generated sample as NumPy .npz format.

It is saved as a NpzFile with keyword: “x”.

Parameters:

filenamestr: The filename to which the sample is saved. .npz will be appended if it isn’t there.
sample_lengthint: A positive integer
initial_valulesnumpy ndarray, optional: 1 dimensional int array whose size coincide with self.c_d_max, by default None. Its elements must be in [0,c_k-1]

See also

numpy.savez_compressed

visualize_model(filename=None, format=None, sample_length=10)#

Visualize the stochastic data generative model and generated samples.

Parameters:

filenamestr, optional: Filename for saving the figure, by default None
formatstr, optional: Rendering output format ("pdf", "png", …).
sample_lengthint, optional: A positive integer, by default 10

See also

graphviz.Digraph

Examples

>>> from bayesml import contexttree
>>> gen_model = contexttree.GenModel(c_k=2,c_d_max=3,h_g=0.75)
>>> gen_model.gen_params()
>>> gen_model.visualize_model()
[1 0 1 0 0 0 1 0 0 0]

class bayesml.contexttree.LearnModel(c_k, c_d_max=2, h0_g=0.5, h0_beta_vec=None, h0_root=None)#

Bases: Posterior, PredictiveMixin

The posterior distribution and the predictive distribution.

Parameters:

c_kint: A positive integer
c_d_maxint, optional: A positive integer, by default 10
h0_gfloat, optional: A real number in \([0, 1]\), by default 0.5
h0_beta_vecnumpy.ndarray, optional: A vector of positive real numbers, by default [1/2, 1/2, … , 1/2]. If a single real number is input, it will be broadcasted.
h0_rootcontexttree._Node, optional: A root node of a superposed tree for hyperparameters by default None

Attributes:

hn_gfloat: A real number in \([0, 1]\)
hn_beta_vecnumpy.ndarray: A vector of positive real numbers.
hn_rootcontexttree._Node: A root node of a superposed tree for hyperparameters.

Methods

`calc_pred_dist`(x)	Calculate the parameters of the predictive distribution.
`estimate_params`([loss, visualize, filename, ...])	Estimate the parameter under the given criterion.
`get_constants`()	Get constants of LearnModel.
`get_h0_params`()	Get the hyperparameters of the prior distribution.
`get_hn_params`()	Get the hyperparameters of the posterior distribution.
`get_p_params`()	Get the parameters of the predictive distribution.
`load_h0_params`(filename)	Load the hyperparameters to h0_params.
`load_hn_params`(filename)	Load the hyperparameters to hn_params.
`make_prediction`([loss])	Predict a new data point under the given criterion.
`overwrite_h0_params`()	Overwrite the initial values of the hyperparameters of the posterior distribution by the learned values.
`pred_and_update`(x[, loss])	Predict a new data point and update the posterior sequentially.
`reset_hn_params`()	Reset the hyperparameters of the posterior distribution to their initial values.
`save_h0_params`(filename)	Save the hyperparameters using python `pickle` module.
`save_hn_params`(filename)	Save the hyperparameters using python `pickle` module.
`set_h0_params`([h0_g, h0_beta_vec, h0_root])	Set the hyperparameters of the prior distribution.
`set_hn_params`([hn_g, hn_beta_vec, hn_root])	Set the hyperparameter of the posterior distribution.
`update_posterior`(x)	Update the hyperparameters using traning data.
`visualize_posterior`([filename, format, h_params])	Visualize the posterior distribution for the parameter.

get_constants()#

Get constants of LearnModel.

Returns:

constantsdict of {str: int, numpy.ndarray}

"c_k" : the value of self.c_k
"c_d_max" : the value of self.c_d_max

set_h0_params(h0_g=None, h0_beta_vec=None, h0_root=None)#

Set the hyperparameters of the prior distribution.

Parameters:

h0_gfloat, optional: A real number in \([0, 1]\), by default None
h0_beta_vecnumpy.ndarray, optional: A vector of positive real numbers, by default None
h0_rootcontexttree._Node, optional: A root node of a superposed tree for hyperparameters by default None

get_h0_params()#

Get the hyperparameters of the prior distribution.

Returns:

h0_paramsdict of {str: float, numpy.ndarray, contexttre._Node}

"h0_g" : the value of self.h0_g
"h0_beta_vec" : the value of self.h0_beta_vec
"h0_root" : the value of self.h0_root

set_hn_params(hn_g=None, hn_beta_vec=None, hn_root=None)#

Set the hyperparameter of the posterior distribution.

Parameters:

hn_gfloat, optional: A real number in \([0, 1]\), by default None
hn_beta_vecnumpy.ndarray, optional: A vector of positive real numbers, by default None
hn_rootcontexttree._Node, optional: A root node of a superposed tree for hyperparameters by default None

get_hn_params()#

Get the hyperparameters of the posterior distribution.

Returns:

hn_paramsdict of {str: float, numpy.ndarray, contexttre._Node}

"hn_g" : the value of self.hn_g
"hn_beta_vec" : the value of self.hn_beta_vec
"hn_root" : the value of self.hn_root

update_posterior(x)#

Update the hyperparameters using traning data.

Parameters:

xnumpy ndarray: 1-dimensional int array

estimate_params(loss='0-1', visualize=True, filename=None, format=None)#

Estimate the parameter under the given criterion.

Parameters:

lossstr, optional: Loss function underlying the Bayes risk function, by default "0-1". This function supports only "0-1".
visualizebool, optional: If True, the estimated context tree model will be visualized, by default True. This visualization requires graphviz.
filenamestr, optional: Filename for saving the figure, by default None
formatstr, optional: Rendering output format ("pdf", "png", …).

Returns:

map_rootcontexttree._Node: The root node of the estimated context tree model that also contains the estimated parameters in each node.

See also

graphviz.Digraph

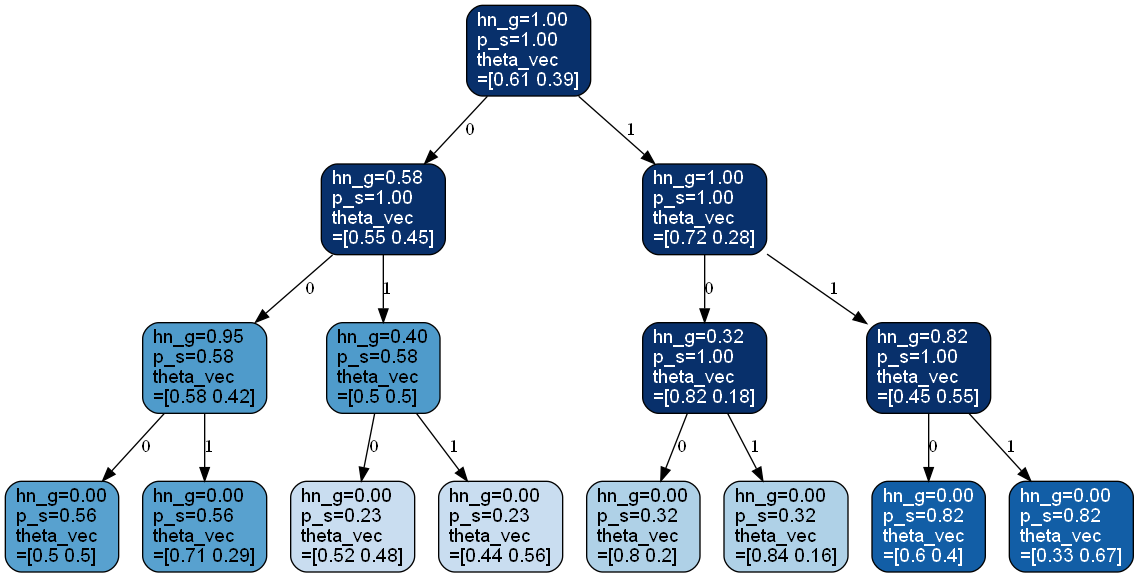
visualize_posterior(filename=None, format=None, h_params=False)#

Visualize the posterior distribution for the parameter.

This method requires graphviz.

Parameters:

filenamestr, optional: Filename for saving the figure, by default None
formatstr, optional: Rendering output format ("pdf", "png", …).
h_paramsbool, optional: If True, hyperparameters at each node will be visualized. if False, estimated parameters at each node will be visulaized.

See also

graphviz.Digraph

Examples

>>> from bayesml import contexttree
>>> gen_model = contexttree.GenModel(c_k=2,c_d_max=3,h_g=0.75)
>>> gen_model.gen_params()
>>> x = gen_model.gen_sample(500)
>>> learn_model = contexttree.LearnModel(c_k=2,c_d_max=3,h0_g=0.75)
>>> learn_model.update_posterior(x)
>>> learn_model.visualize_posterior()

get_p_params()#

Get the parameters of the predictive distribution.

Returns:

p_paramsdict of {str: numpy.ndarray}

"p_theta_vec" : the value of self.p_theta_vec

calc_pred_dist(x)#

Calculate the parameters of the predictive distribution.

Parameters:

xnumpy ndarray: 1-dimensional int array

make_prediction(loss='KL')#

Predict a new data point under the given criterion.

Parameters:

lossstr, optional: Loss function underlying the Bayes risk function, by default “KL”. This function supports “KL” and “0-1”.

Returns:

predicted_value{float, numpy.ndarray}: The predicted value under the given loss function. If the loss function is “KL”, the predictive distribution will be returned as a 1-dimensional numpy.ndarray that consists of occurence probabilities.

pred_and_update(x, loss='KL')#

Predict a new data point and update the posterior sequentially.

Parameters:

xnumpy.ndarray: 1-dimensional int array
lossstr, optional: Loss function underlying the Bayes risk function, by default “KL”. This function supports “KL”, and “0-1”.

Returns:

predicted_value{float, numpy.ndarray}: The predicted value under the given loss function.

bayesml.contexttree package

Contents

bayesml.contexttree package#

Module contents#